آیا تا کنون به طلوع دو خورشید در آسمان فکر کردهاید؟ چیزی مشابه آنکه در اولین فیلم جنگهای ستارهای نشان داده شد. دو خورشید که با فاصله کمی در آسمان پدیدار شده و در پایان روز، باعث ایجاد دو غروب زیبا شوند. یا حتی با غروب یکی، خورشید دیگر طلوع کند! آیا اصلا امکان شکلگیری سیاره در چنین منظومههای شامل یک ستاره دوتایی وجود دارد؟ آیا حیات هم میتواند روی آنها شکل بگیرد؟
میلیونها سیاره در راه شیری
واقعیت این است که سیارات میتوانند در سیستمهای ستارهای دوتایی وجود داشته باشند. حتی تعداد زیادی از این سیارات رصد شدهاند. به طور مثال kepler 47-c سیارهای با پنج برابر جرم زمین است که در مداری مشابه مدار زمین در گردش است. اما تفاوت اینجاست که به جای یک ستاره، دو ستاره در آسمان آن دیده میشود. اما در مورد وجود حیات در سطح آن نباید زیاد امیدوار بود. چرا که این سیاره به احتمال زیاد، گازی شکل است.
ستارهشناسان به طور دقیق نمیتوانند از تعداد سیارات در اینچنین سیستمهای چند ستارهای، تخمینی داشته باشند. در حقیقت ما هنوز از تعداد کل سیارات، در هر نوع منظومه ستارهای نیز اطلاع دقیقی در دست نداریم. با این حال آنچه مشخص است، این حقیقت است که تعداد سیارات در همین کهکشان راه شیری بسیار بسیار زیاد است. عددی در حدود چند صد میلیون سیاره که چند میلیون مورد از آنها قابلیت میزبانی از حیات را میتوانند داشته باشند.
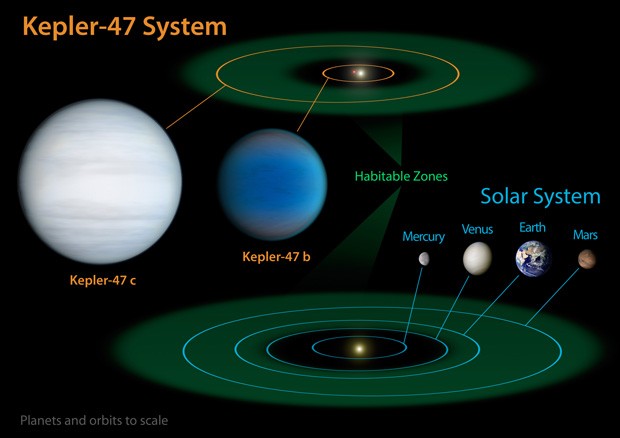
مقایسه ستاره دوتایی کپلر 47 و دو سیاره اطراف آن. در بخش پایین نیز سامانه خورشیدی نشان داده شده است. در هر دو مورد، ناحیه سبزرنگ، کمربند حیات را نشان میدهد.
اما باید توجه داشته باشیم که سیارات را نمیتوان در هر جای دلخواهی قرار داد. به خصوص در مورد یک ستاره دوتایی وضعیت پیچیدهتر است و بسیاری از مدارها پایدار نخواهند بود. مهمترین عاملی که در این پایداری نقش دارد، باز هم نیروی گرانش است.
و باز هم گرانش
ما معمولا در مورد گرانش بسیار سادهانگارانه فکر میکنیم. دو جرم همدیگر را جذب میکنند و تمام. اگر جرمی را رها کنیم به سطح زمین میافتد و اگر موتور سفینه فضایی را روشن کنیم میتواند از دام جاذبه گرانشی زمین رها شود. اما در واقعیت، نقش گرانش بسیار پیچیدهتر از اینهاست.
البته درست است که گرانش در مواردی که تنها دو جرم با هم واکنش دارند، ساده است. به طور مثال سیارهای که به دور یک ستاره تک در چرخش است. حتی نوشتن محاسبات ریاضی مربوط به مدارهای پایدار در اطراف این ستاره کار چندان سختی نیست. اما وقتی که جرم سومی وارد این محدوده میشود، دیگر با فرآیند سادهای روبرو نیستیم. این جرم سوم میتواند یک سیاره یا حتی ستاره دیگر باشد. افراد زیادی از سالها پیش بر روی مسئله سه جرمی وقت گذاشتند که یکی از اولین آنها هنری پوانکاره (Henri poincare) بود. شاید چشمان خیره پوانکاره سختی ریاضیات درگیر در این مسئله را به ما نشان میدهد!
منظور این نیست که پایداری در سیستمهای چند جرمی غیرممکن است. خود منظومه خورشیدی ماشامل یک ستاره، هشت سیاره و تعداد زیادی سیارک و همینطور سیاره کوتوله است و میدانیم که در طی سالیان طولانی گذشته، اتفاق خاصی برای مدارهای پایدار این اجرام نیفتاده است. اما مسئله در اینجا این است که هر جرمی به طور کلی تحت تاثیر گرانش تنها یک جرم بالاتر از خود است. ماه تحت گرانش زمین است و زمین تحت گرانش خورشید گردش میکند. به این صورت تاثیر سیاره عطارد روی نوع مدار قمر ماه به دور زمین را کاملا میتوان صفر در نظر گرفت.
در نتیجه تمامی اندرکنشهای گرانشی در منظومه خورشیدی را میتوانیم یک به یک در نظر بگیریم. اینگونه هر جرمی مدار پایدار خود به دور جرم بزرگتر را برای میلیونها سال حفظ کرده و خواهد کرد. اما اگر سیاره مشتری را در محل کنونی سیاره مریخ قرار دهید، یا آن را در مدار خودش ده بار پرجرمتر کنید، این رویه سلسله مراتبی به هم میریزد. زیرا در این صورت دیگر نمیتوان برای پیشبینی شکل مدار زمین، تنها نقش خورشید را در نظر گرفت و از مشتری چشمپوشی کرد.
هدف از توضیح این نظام سلسه مراتبی در منظومه خورشیدی این بود که بگوییم در مورد ستارههای دوتایی، اگر سیارهای بخواهد در اطراف آنها گردش کرده و برای مدتهای طولانی در مدار خودش پایدار باقی بماند، انتخابهای بسیار کمتری خواهد داشت. بسیاری از مدارهایی که در اطراف یک ستاره تک پایدار محسوب میشد، حال با وجود حتی یک ستاره کمجرم، دیگر پایدار نخواهد بود. حتی بادهای ستارهای ناشی از ستاره دوم، میتواند سیاره را از منظومه خارج کرده یا باعث برخورد آن به جرم دیگری شود.
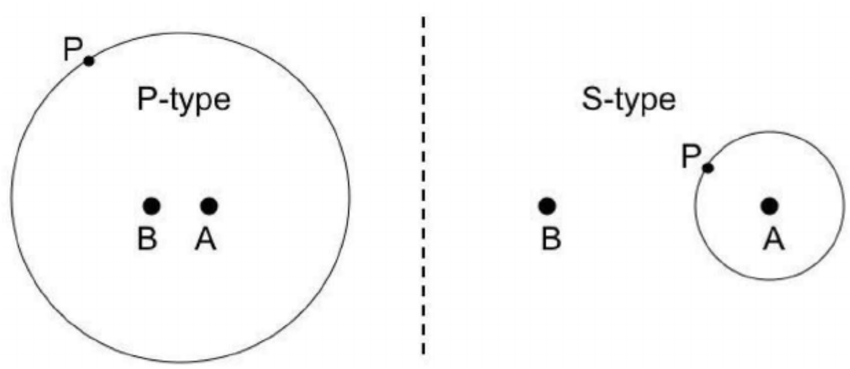
به طور کلی مدار یک سیاره در ستاره دوتایی به دو شکل میتواند پایدار باشد. 1. در فاصله نزدیک به یکی از ستارهها قرار گرفته و تنها به دور آن ستاره تک گردش کند. 2. در فاصله دورتر قرار داشته و به دور هر دو ستاره (به دور مرکز جرم مشترک آنها) در چرخش باشد. در این شکل A و B نمایانگر ستاره و P نشاندهنده یک سیاره است.
چنین سیارهای تنها دو انتخاب خواهد داشت. اول اینکه سیاره میتواند در فاصله بسیار کمی از یکی از ستارهها در گردش باشد. اینگونه نیروی گرانشی غالب، نیروی وارد آمده از ستاره نزدیکتر است و می توان از نقش ستاره دوم تا حد خوبی چشمپوشی کرد. حالت دیگر این است که سیاره در فواصل زیاد قرار داشته و به دور مجموعه این دوستاره (در واقع به دور مرکز جرم مشترکشان) در گردش باشد. همه این موارد تنها برای ستارههای دوتایی گفته شد. وضعیت برای سامانههای شامل سه یا تعداد بیشتر ستاره به حدی پیچیده است که بهتر است اصلا وارد بحث آنها نشویم!
رقص دو ستاره
اگ سیاره kepler 47-c را در نظر بگیریم، مشابه مورد دومی است که به آن اشاره کردیم: دو ستاره که در فاصله بسیار نزدیک از یکدیگر قرار گرفته و به سرعت به دور یکدیگر می چرخند و سیارهای که در فاصله بسیار دور به دور هردوی آنها در گردش است. اینجا برای سیاره اهمیتی ندارد که دو ستاره در مرکز این منظومه قرار گرفتهاند. سیاره اینطور حس میکند که انگار یک ستاره پرجرمتر در مرکز جرم این دو ستاره قرار گرفته و تنها آن ستاره فرضی است که بر روی مدار سیاره اثر میگذارد.
حالت دیگری که برشمردیم نزدیکی خیلی زیاد سیاره به یکی از ستارهها است. ستاره دوم یا آنقدر دور است که اثر چندانی بر مدار سیاره نگذارد، یا آنقدر کمجرم است که باز هم قادر نیست اختلالی در پایداری مدار سیاره ایجاد کند.
در مجموع باید گفت که وجود سیارات اطراف ستارههای تک، محتملتر است. اما از طرف دیگر، بخش زیادی از ستارههای آسمان، در واقع ستاره دوتایی یا چندتایی هستند. به این صورت اگر حتی درصد کمی از آنها شامل سیاره باشند، در مجموع سیستمهای دوتایی بسیاری وجود خواهند داشت که شامل یک یا چند سیاره در اطراف خود هستند.
حیات در سامانه ستاره دوتایی
اما در مورد آب و هوا و شکلگیری حیات در چنین سیاراتی چه میتوان گفت؟ پاسخ به این سوال کمی مشکلتر است. چرا که رسیدن به تعریفی جامع که شامل تمامی حالات شکلگیری حیات شود، دشوار است. به خصوص در چنین سیستمهایی که گرمای هر دو ستاره به سیاره میرسد.
مدلهایی وجود دارد که محدوده کمربند حیات را در چنین سیستمهایی مشخص میکنند. یعنی جایی که آب به صورت مایع میتواند جریان داشته باشد. اما تضمینی وجود ندارد که این مدلها کاملا دقیق باشند، چرا که اگر برخی از فرضها را تغییر دهیم، محدوده مورد نظر تفاوت قابل توجهی خواهد کرد.
به علاوه اگر حالت چرخش به دور یک ستاره را در نظر بگیریم، در چنین سیارهای گاهی دو ستاره در آسمان خواهد بود و گاهی نیز در هر دو سمت سیاره خورشیدی در حال تابیدن بر سطح سیاره است. یعنی در چنین وضعیتی دیگر شبی وجود نخواهد داشت و تمامی شبانهروز در روشنایی سپری میشود!
اگر به اشکال پیچیده حیات که بر روی زمین وجود دارد فکر کنیم، شکلگیری آنها بر روی چنین سیارهای را سخت بتوان تصور کرد. با این حال طبیعت کیهان، نشان داده است که همواره باعث شگفتی ما میشود و این تنها کمبود آگاهی ما از درک کامل ساز و کار آن است که مواردی را غیرممکن یا بسیار نامحتمل میدانیم. در حالی که پس از چندی خلاف آن ثابت میشود.
 گجت نیوز آخرین اخبار تکنولوژی، علم و خودرو
گجت نیوز آخرین اخبار تکنولوژی، علم و خودرو 







